- Detalles
- Escrito por José Miguel Contreras
- Categoría: Glosario
El porcentaje de tiro real (PTR), True Shooting Percentage (TS%), es una medida de la eficiencia de los lanzamientos que tiene en cuenta los tiros de campo de 2 puntos, los tiros de campo de 3 puntos y los tiros libres. Es decir, el porcentaje real de tiros es una métrica que además del desempeño de un jugador o de un equipo en el campo tiene en cuenta la eficacia en la línea de tiros libres, es decir, considera la eficiencia en todo tipo de lanzamientos.
PTR (TS%) considera el número de puntos que un jugador (o equipo) anotó en relación con las posesiones de tiro que utilizó, abarcando los tiros de campo intentados, así como los tiros libres intentados. El coeficiente 0,44 corrige los los tiros libres intentados para reflejar el hecho de que a menudo se toman en parejas, así como en otras situaciones como tiros libres adicionales o faltas técnicas.
Una característica del PTR (TS%) es que calcula la producción ofensiva de un jugador frente a las posesiones de tiro que usó para llegar allí, independientemente del tipo de posesión (dos puntos, tres puntos o tiros libres) que usara el jugador.
El PTR (TS%) es valioso para considerar todo tipo de jugadores, pero es especialmente útil cuando se analizan hombres grandes, que normalmente no lanzan muchos triples, un sólido PTR de un hombre grande revela que probablemente juega cerca del aro, y puede atraer faltas personales con un porcentaje aceptable.

- Detalles
- Escrito por José Miguel Contreras
- Categoría: Glosario
Una alternativa a los indicadores valoración (V o PIR) y al de Eficiencia (EFF), ampliamente utilizado en diferentes ligas, por ejemplo la NBA, es la ratio de eficiencia del jugador "Player Efficiency Rating" (PER) desarrollado por John Hollinger.
Este indicador mide el rendimiento por minuto de un jugador ajustado al ritmo (pace) de juego. La particularidad del PER es que Hollinger lo definió de manera que el “PER promedio” permite realizar comparaciones del rendimiento de los jugadores a lo largo de las temporadas, tomando como 15, el valor de referencia (termino medio).
El PER tiene en cuenta tanto acciones positivas: tiros de campo convertidos, tiros libres convertidos, asistencias, rebotes totales, tapones a favor y balones robados, y como acciones negativas: tiros de campo fallados, tiros libres fallados, balones perdidos y faltas personales en contra. El resultado final es una evaluación sumativa de éstas, ajustada en base al tiempo que cada jugador participa en el partido y al ritmo (pace), lo que permite, por ejemplo, comparar jugadores titulares o de banquillo.
Está métrica permite también resumir los logros para una temporada concreta en un solo valor y clasificar éstos en una determinada escala.
| Escala | Puntuación |
| Mejores temporadas de todos los tiempos | >35 |
| Candidato real a MVP de la temporada | 30 a 35 |
| Fuerte candidato a MVP | 27.5-30 |
| Candidato débil a MVP | 25-27.5 |
| All-Star | 22.5-25 |
| Posible All-Star | 20-22.5 |
| Segunda opción ofensiva | 18-20 |
| Tercera opción ofensiva | 16.5-18 |
| Jugador ligeramente por encima de la media | 15-16.5 |
| Jugador de rotación | 13-15 |
| Jugador que puede entrar en la rotación | 11-13 |
| Jugador marginal | 9-11 |
| Jugador que no se quedará en la liga | 0-9 |

¿Cómo calculamos el PER?
Todos los cálculos comienzan con lo que se llama "PER no ajustado" (uPER). La fórmula es:
Cuando se multiplica y se refactoriza, la ecuación anterior se convierte en:
Donde
Donde:
tm el prefijo, que indica el equipo en lugar del jugador;
lg el prefijo, que indica liga en lugar de jugador;
Minutos para el número de minutos jugados;
VOP - valor de posesión (en referencia a la liga)
Una vez que se calcula el uPER, este debe ajustarse al ritmo (pace) del equipo y normalizarse a la liga para convertirse en PER:

Este paso final quita la ventaja que tienen los jugadores cuyos equipos juegan un estilo rápido de baloncesto, Fast break, (y por lo tanto tienen más posesiones y más oportunidades para tener una mayor frecuencia de acciones positivas o negativas).
- Una de las problemáticas del PER para las temporadas de la NBA anteriores a 1978, es la no existencia de datos sobre balones perdidos.
- También existen ciertos artículos, como el de Josh Gonzales, que muestran otras problemáticas de este índice, tales como:
- No ser lo suficientemente específico: Según el autor, si John Hollinger hubiera sido más específico en la metodología del PER, se podría comprobar si el PER es o no una medida efectiva.
- No reportar significado y tamaños de efecto: Dado que el modelo de Hollinger no tiene variables de resultado específicas, no hay hallazgos reportados. Por ejemplo, las web que usan PER, no informan si el PER predice significativamente las victorias, o el porcentaje de victorias predice o cualquier otro hallazgo con respecto a las posibles variables de resultado.
- No se actualiza en función de los datos: la métrica no ha cambiado desde su creación.
- PER mide en gran medida el rendimiento ofensivo. Hollinger admite que dos de las estadísticas defensivas que incorpora -tapones a favor y balones robados (que no fueron registrados como un estadísticas oficiales hasta 1973)- pueden producir una imagen distorsionada del valor de un jugador y que el PER no es una medida fiable de la habilidad defensiva de un jugador.
- Ciertos especialistas han argumentado que el PER da un peso indebido a la contribución de un jugador con minutos limitados, o contra la segunda unidad de un equipo, y subestima a los jugadores que tienen suficiente diversidad en su juego para jugar los minutos de inicio.
- No es pertinente comparar jugadores de diferentes generaciones utilizando el PER, esto se debe principalmente a los cambios en las reglas y a los cambios en los datos estadísticos recopilados en diferentes épocas.
Se ha dicho que el PER recompensa a los lanzadores ineficientes. Nota de Dave Berri, autor de The Wages of Wins:
Como indica basketball-reference , una solución en el caso de que falten datos en ciertas temporadas es:
- Asignar el valor 0 a T3C , BP, TF y BP.
- Establecer el valor de posesión de la liga (VOP) igual a 1.
- Establecer el porcentaje de rebote defensivo (%RD) igual a 0,7.
- Establecer rebotes ofensivos del jugador (RO) igual a 0.3 * RT.
Referencias
Basketball-reference (2021). Calculating PER. Recuperado de https://www.basketball-reference.com/about/per.html
Cerynik, D. L., Lewullis, G. E., Joves, B. C., Palmer, M. P., & Tom, J. A. (2009). Outcomes of microfracture in professional basketball players. Knee Surgery, Sports Traumatology, Arthroscopy, 17(9), 1135-1139. ver.
- Detalles
- Escrito por José Miguel Contreras
- Categoría: Glosario
Siguiendo la metodología de Oliver (2004) y Caliwag et al. (2018), los cuatro factores son las métricas derivadas de los resúmenes estadísticos tradicionales que se correlacionan mas estrechamente con ganar partidos de baloncesto. Identificando las fortalezas y debilidades estratégicas de un equipo. Por lo que predecir el ganador en un partido también puede estar relacionado con los cuatro factores. Se pueden aplicar los cuatro factores tanto al ataque como a la defensa de un equipo (es decir, tenemos ocho factores), no siendo todos equivalentes en valor.
Podemos encontrar equipos donde sus jugadores pueden obtener mejores resultados que sus oponentes en tres de estos factores y aun así perder, o ser considerados equipos mediocres, o, todo lo contrario. Es por ello que identificar los factores que son importantes ayuda a identificar una estrategia para construir un equipo exitoso.
Las formulas siguientes son el valor ponderado de cada factor (Caliwag et al., 2018), donde los autores consideran el "tiro", Porcentaje Efectivo de Tiro de Campo (PETC), el factor más importante, seguido de las "pérdidas de balón", Tasa de Perdidas (TP), "rebotes", Porcentaje de Rebote Ofensivo (PRO) y "tiros libres", Tasa de tiros libres (TTL), asignando unas proporciones de importancia para la victoria del 40%, 25%, 20% y 15% respectivamente (Oliver, 2004):
Donde:
TCCE = Tiros de Campo Convertidos (Equipo)
TCC3E = Tiros de Campo Convertidos de tres puntos (Equipo)
TCIE = Tiros de Campo Intentados (Equipo)
PERE = Pérdidas (Equipo)
TLIE = Tiros Libres Intentados (Equipo)
ROE = Rebotes ofensivos (Equipo)
ROO = Rebotes ofensivos (Oponente)
El primer factor, y más importante, es, como indica la lógica, meter el mayor número de canastas de las que se intentan. El Porcentaje efectivo de tiro de campo (PETC) se considera un estimador más útil que el Porcentaje de Tiros de Campo (PTC), ya que este último combina de igual manera tiros de 2 y 3 puntos, no permitiendo evaluar de forma separada la eficiencia en distintos tipos de jugadores. Por ejemplo, no es lo mismo un especialista de tres puntos que un cinco clásico.
Otra forma de calcular este factor, tanto a nivel equipo como jugador individual, es mediante la fórmula:
Donde:
TCC2E = Tiros de Campo Convertidos de dos puntos (Equipo)
TCC3E = Tiros de Campo Convertidos de tres puntos (Equipo)
TCIE = Tiros de Campo Intentados (Equipo)
En este caso cambia la ponderación del tiro de 3 puntos de 0,5 a 1,5 ya que un tiro de tres puntos convertido equivale a 1,5 veces un tiro de dos convertido. Los resultados de ambas fórmulas son equivalentes.
A continuación, mostramos un ejemplo, tomando como referencia los resultados de la temporada 2020-2021 de la Euroleague (www.euroleague.net), en el que se comparan los Porcentaje de 2 puntos (%2P), Porcentaje de 3 puntos (%3P), Tiros de Campo Convertidos (TCCE), Porcentaje Efectivo de Tiro de Campo (PETC) y Porcentaje de Tiro Verdadero (PTV), que según la Euroleague se define como:
Estas métricas nos van a permitir comparar los distintos equipos de esta competición y sacar alguna conclusión de estos porcentajes. Por ejemplo, tomamos dos equipos cuyos resultados han sido muy diferentes en esta temporada FC Barcelona (subcampeón de la competición, que terminó primero en la fase regular) y Khimki Moscow Region (último clasificado en la fase regular). Respecto al FC Barcelona, como se muestra en la Tabla1, éste ocupa la 7ª posición en porcentaje de dos puntos (%2P), la 4ª en porcentaje de tres puntos (%3P), la 3ª posición en porcentaje de tiros de campo convertidos (PTCC ó %PCC), la 6ª posición en porcentaje efectivo de tiro de campo (PETC o %PETC) y, por último, la 3ª posición en porcentaje de tiro verdadero (PTV ó %PTV). Por el contrario, el Khimki ocupa la 16ª posición en porcentaje de dos puntos (%2P), la 18ª en porcentaje de tres puntos (%3P), la 18ª posición en porcentaje de tiros de campo convertidos (PTCC ó %PCC), la 18ª posición en porcentaje efectivo de tiro de campo (PETC o %PETC) y, por último, la 18ª posición en porcentaje de tiro verdadero (PTV ó %PTV). Como vemos, estos porcentajes, afectan, aunque no sean la causa última de la clasificación, a los resultados obtenidos. Pero como lo importante en este deporte es meter canastas, cuanto más mejor de las que se intentan, un buen porcentaje en estas métricas afectará a la posición en la tabla. Hay que destacar que, aunque el FC Barcelona quedó primero en la tabla, en estás métricas es superado por los dos equipos turcos Anadolu Efes Istanbul (campeón del torneo) y Fenerbahce Beko Istanbul (que llegó a la Final Four esa temporada), debido al menor porcentaje de tiro de dos puntos.
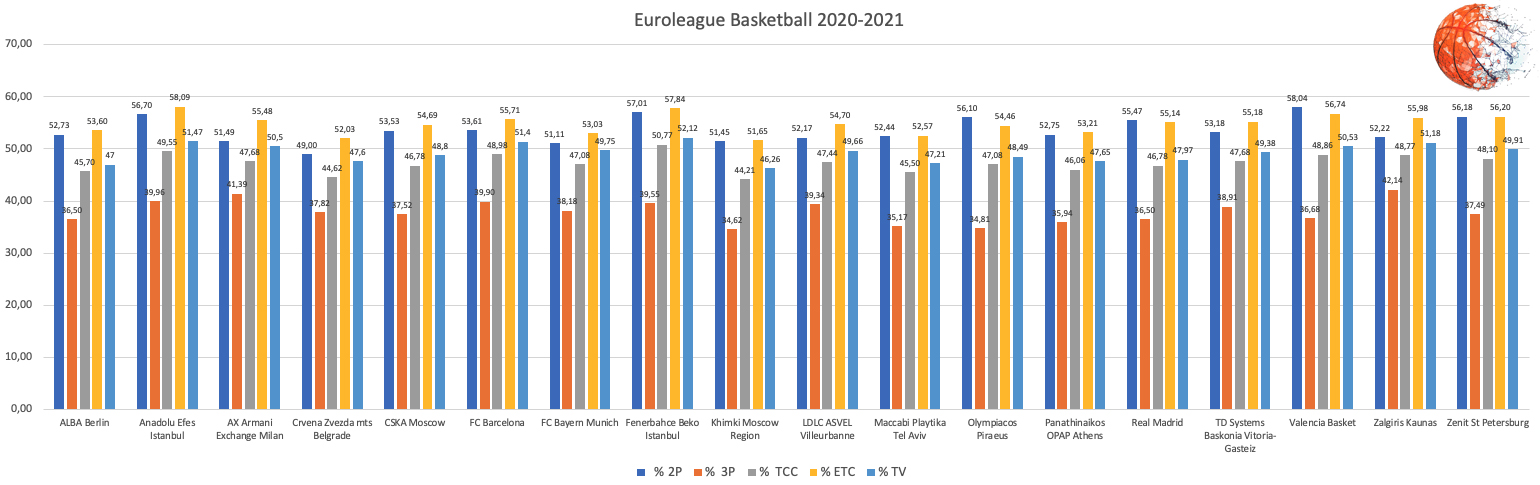
Figura 1. Comparación porcentajes 2 puntos, 3 puntos, Titos de Campo Convertidos, Efectivo Tiro de Campo y Tiro Verdadero
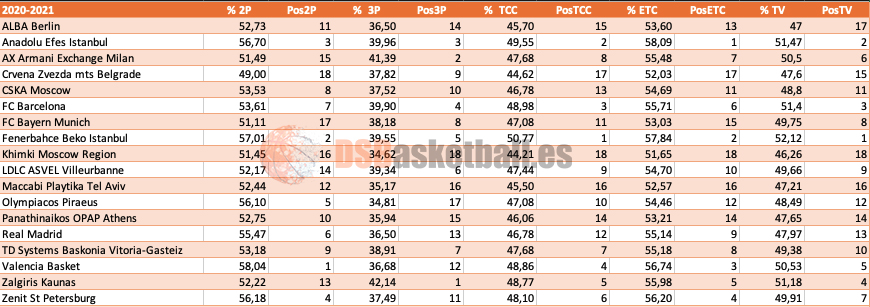
Tabla 1. Comparación porcentajes 2 puntos, 3 puntos, Titos de Campo Convertidos, Efectivo Tiro de Campo y Tiro Verdadero, y posición por métrica, Euroleague 2020-2021
El segundo factor evalúa cuántas posesiones “regala” un equipo al rival. Cada pérdida termina una posesión sin tiro (o con un tiro de muy baja calidad) y, además, suele generar puntos en transición del oponente. Por eso, incluso equipos muy eficientes en el tiro pueden perder si su volumen de pérdidas es alto.
Una forma estándar (tempo-free) de medirlo es la Tasa de Pérdidas o Turnover Percentage (TOV%), entendida como el porcentaje de “acciones de ataque” que terminan en pérdida:
donde el factor 0.44 aproxima el “coste medio” de los tiros libres en términos de posesión.
Interpretación directa:
-
TP baja ⇒ el equipo finaliza más posesiones con tiro (o al menos con opción de tiro).
-
TP alta ⇒ necesitas “compensar” con mucho acierto o rebote ofensivo para sostener la eficiencia.
Aplicación defensiva (forzar pérdidas):
En defensa, el análogo es “hacer que el rival pierda más”, es decir, aumentar la TP del oponente mediante presión al balón, negar líneas de pase, traps selectivos, etc. Aquí hay un matiz táctico importante: forzar pérdidas puede incrementar el riesgo de faltas o desajustes defensivos si se sobre-presiona.
El tercer factor mide la capacidad de un equipo para alargar posesiones capturando rebotes en ataque. Es una fuente clásica de ventaja porque convierte un fallo de tiro en una “segunda oportunidad”.
La forma habitual de expresarlo es el Porcentaje de Rebote Ofensivo (PRO u OREB%):
donde RDO son los rebotes defensivos del oponente (en muchos boxscores no aparece como tal; suele obtenerse como RDO = Rebotes Totales del oponente − Rebotes Ofensivos del oponente). La idea clave es que el denominador representa los rebotes disponibles en el aro rival.
Interpretación directa:
-
PRO alta ⇒ más segundas oportunidades, más tiros por partido (sin necesidad de subir el ritmo).
-
PRO baja ⇒ dependes más del acierto inicial y de evitar pérdidas.
Aplicación defensiva:
El equivalente defensivo es asegurar el rebote (bajar el PRO del rival), es decir, maximizar el rebote defensivo y cerrar el aro. En términos de “ocho factores”, se suele hablar de evitar segundas oportunidades como pilar defensivo.
El cuarto factor captura la habilidad para generar tiros libres. Los tiros libres tienden a ser una vía eficiente de anotación y además producen efectos indirectos: cargan de faltas al rival, condicionan rotaciones y reducen agresividad defensiva.
Una medida muy extendida es la Free Throw Attempt Rate, equivalente a tu TTL:
Interpretación directa:
-
TTL alta ⇒ el equipo ataca el aro, fuerza contactos, suma puntos “baratos”.
-
TTL baja ⇒ el ataque depende más del tiro en juego (y de su varianza).
Aplicación defensiva:
El análogo defensivo es no conceder tiros libres (reducir la TTL del oponente): buena verticalidad, disciplina en closeouts, evitar llegar tarde a las ayudas, etc.
Referencias
Caliwag, J. A., Aragon, M. C. R., Castillo, R. E., & Colantes, E. M. S. (2018, April). Predicting Basketball Results Using Cascading Algorithm. In Proceedings of the 2018 International Conference on Information Science and System (pp. 64-68).
Oliver, D. (2004). Basketball on paper: rules and tools for performance analysis. Potomac Books, Inc..
- Detalles
- Escrito por José Miguel Contreras
- Categoría: Glosario
En el mundo del deporte, un box-score es una tabla resumen de estadísticas (métricas) estructurada que muestran el desempeñó de cada jugador y los globales del cada equipo en un partido.

Box-Score partido de los 100 puntos de Wilt Chamberlain's
En baloncesto, un box-score resume ciertas métricas, absolutas y relativas, obtenidas mediante observaciones objetivas que nos permiten realizar comparaciones, y dar contexto, entre jugadores, del mismo equipo o rivales.
Algunos de los campos o métricas que podemos encontrar en un box-score son las siguientes:
- Dorsal.
- Nombre.
- 5 inicial. Si el jugador ha sido seleccionado para el quinteto titular del encuentro.
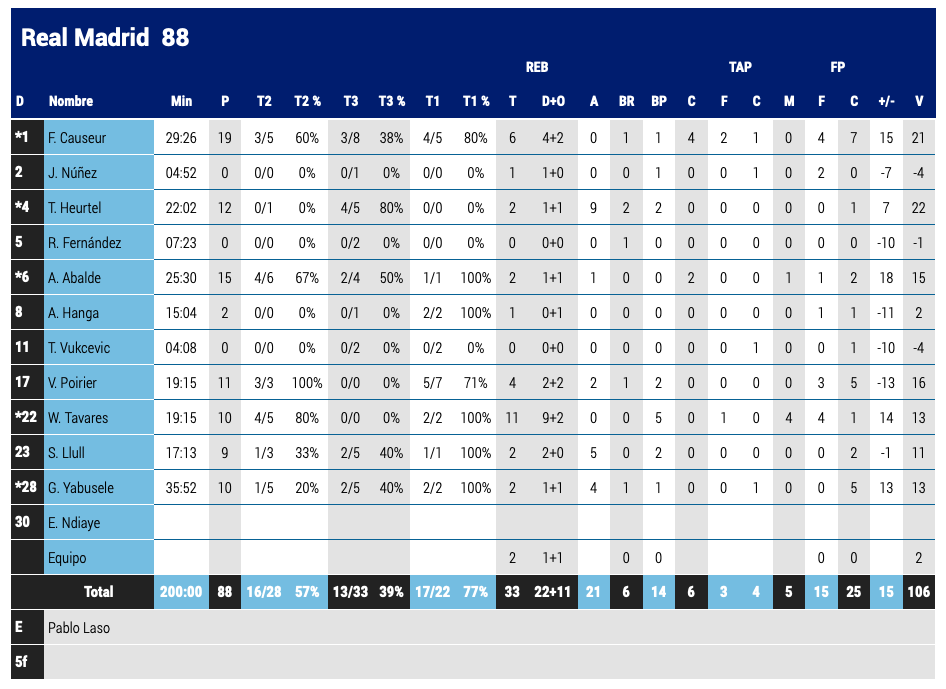
- Minutos. Indica los minutos jugados por el jugador en cuestión. En esta métrica hay que tener en cuenta el formato de esta variable, puede aparecer en formato mm:ss (minutos:segundos) o en mm (minutos), en este caso, los decimales indican la proporción de minutos que representan los segundos jugados (10.25 representa 10 minutos y 15 segundos). Normalmente la última final indica el total del equipo, en el caso de competiciones FIBA el total será de 200:00 (minutos:segundos) y de 240:00 en el caso de competiciones como la NBA. Esta métrica nos va a permitir realizar segmentaciones y métricas relativas en función del tiempo jugado.
- Puntos (P). Métrica absoluta que indica el total de puntos anotados por un jugador. Refiere a la fórmula (2 x Tiros de 2 Convertidos (T2C) + 3 x Tiros de 3 Convertidos (T3C) + Tiros de 1 Convertidos (T1C)).
T2C = Tiros de 2 Convertidos
T3C = Tiros de 3 Convertidos
T1C = Tiros de 1 Convertidos

- Tiros de Dos Puntos Convertidos (T2C). Métrica absoluta que indica el número de canastas de dos puntos convertidas por el jugador. Un tiro de dos convertido (MGF2 en inglés) se asigna a un jugador cada vez que un T2I realizado por él da como resultado una canasta o se le ha sido concedido debido a una interferencia ilegal del balón por parte de un defensor.
- Tiros de Dos Puntos Intentados (T2I). Métrica absoluta que indica el número de canastas de dos puntos intentadas por el jugador. Un Tiro de 2 puntos Intentado (FGA2 en inglés) se asigna a un jugador cada vez que tira, lanza o empuja un balón vivo (el balón está en juego) a la canasta de su oponente en un intento de anotar, en este caso de dos puntos, independientemente de la consecución de la acción.
* En algunos casos, estas métricas aparecen como T2 (T2C/T2I).
- T2%. Porcentaje de Tiros de dos Puntos. Métrica relativa que indica:
-
\[ T2\% = \frac{T2C}{T2I} \times 100\]
- Tiros de Tres Puntos Convertidos (T3C). Métrica absoluta que indica el número de canastas de tres puntos convertidas por el jugador. La interpretación es análoga al caso del T2C.
- Tiros de Tres Puntos Intentados (T3I). Métrica absoluta que indica el número de canastas de tres puntos intentadas por el jugador. La interpretación es análoga al caso del T2I.
* En algunos casos, estas métricas aparecen como T3 (T3C/T3I).
- T3%. Porcentaje de Tiros de tres Puntos. Métrica relativa que indica:
- Tiros de Un Punto Convertidos (T1C). Métrica absoluta que indica el número de tiros libres convertidos por el jugador.
- Tiros de Un Punto Intentados (T1I). Métrica absoluta que indica el número de tiros libres intentados por el jugador. Un T1I (FTA en inglés) se asigna a un jugador cuando ese jugador lanza un tiro libre, a menos que haya una violación por parte de un jugador defensivo y el tiro resulte fallado (si encesta, si se le asigna).
* En algunos casos, estas métricas aparecen como T1 (T1C/T1I).
- T1%. Porcentaje de Tiros de un Punto. Métrica relativa que indica:

- Rebotes. Métricas absolutas que indican la recuperación controlada de un balón vivo por un jugador, o un equipo que tiene derecho sacar el balón, después de un tiro de dos o de tres fallado o del último tiro libre intentado. Se descomponerse en:
- Rebotes Totales (RT). Métrica absoluta que indica la suma de rebotes defensivos y ofensivos.
- Rebotes Defensivos (RD). Métrica absoluta que indica la suma de rebotes defensivos. Los rebotes defensivos son asignados cuando la posesión la gana un jugador de un equipo (o el equipo, si el tiro intentado salió fuera, ocurra una falta antes de que se obtenga el control del balón, ...) que no intentó anotar.
- Rebotes Ofensivos (RO). Métrica absoluta que indica la suma de rebotes ofensivos. Los rebotes ofensivos son asignados cuando la posesión es retenida por un jugador del mismo equipo que falló el T1I, T2I o el T3I. Se asigna el rebote al equipo en el caso de que se produzca una propia canasta durante una situación de rebote (un jugador defensivo mete el balón accidentalmente en su propia canasta).
- Asistencias (A). Métrica absoluta que indica el nº de pases que permiten o facilitan a otro jugador encestar.
- Balones Robados (BR). Métrica absoluta que indica el nº de balones robados o recuperados por el jugador. Los robos se asignan cuando un jugador defensivo causa la pérdida de balón, aunque no sea el beneficiario último de la perdida o la posesión no sea considerada como pelota viva.
- Balones Perdidos (BP). Métrica absoluta que indica el nº de errores de un jugador o equipo que da como resultado que el equipo defensivo obtenga la posesión del balón. Una pérdida de balón solo puede ser cometida por el equipo que tiene el control del balón. Pueden ser debidos a un mal pase, un mal manejo del balón que queda suelto o cualquier tipo de infracción o falta ofensiva que implique el cambio de posesión.

- Tapones a Favor (TF). Métrica absoluta que indica el nº de tiros bloqueados por un jugador cada vez que hace contacto apreciable con el balón para alterar la trayectoria de un T2I o T3I y este es fallado. En este caso el balón puede haber salido o no de la mano del tirador para que se cuente el tapón.
- Tapones en Contra (TC). Métrica absoluta que indica el nº de tiros intentados por un jugador que han sido bloqueados por un jugador del equipo contrario.
- Faltas Personales en Contra (FC). Métrica absoluta que indica el nº de faltas sancionadas por la decisión de un árbitro. En este apartado se aglutinan faltas personales, técnicas, antideportivas y descalificantes asignadas a un determinado jugador. Las faltas técnicas y descalificantes también se pueden sancionar al entrenador o al banquillo, siendo importante diferenciar estos tipos, ya que las faltas técnicas y descalificantes sancionadas al entrenador o al banquillo se registran contra el entrenador y no se cuentan como faltas de equipo.
- Faltas Personales a Favor (FF). Métrica absoluta que indica el nº de faltas que comete el equipo contrario hacia un jugador. En el caso de una falta descalificante, si la falta se comete físicamente sobre un jugador, se asigna también como falta personal al jugador que ha sido objeto de ella.
- Mates (M). Métrica absoluta que indica el nº de T2C en la que un jugador lleva el balón por encima del aro y lo introduce contra el aro con una o dos manos en las que ésta o éstas golpean la parte superior del aro.
- Valoración (V). En algunas competiciones como la ACB se utiliza la métrica indirecta "índice de valoración" del jugador para comparar rendimientos globales de éstos en función de métricas positivas (Puntos + Rebotes Totales + Asistencias + Balones Robados + Tapones a favor + Faltas Personales en Contra) y métricas negativas (Tiros de Campo Fallados + Tiros Libres Fallados + Tapones Recibidos + Balones Perdidos + Faltas Personales a Favor). Su formulación es la siguiente:
* En algunos casos, podemos encontrar este índice con las siglas PIR (Performance Index Rating).
- Más/Menos (+/-). Este índice mide el rendimiento de un jugador en función de los puntos a favor y en contra que ha obtenido un equipo con un jugador concreto en cancha. Es decir, mide la influencia de un jugador sobre el rendimiento de su equipo, a partir de la diferencia de los puntos que anota y recibe un equipo mientras dicho jugador está en la pista. Según la ACB, "la estadística más/menos es un termómetro de lo que puede haber aportado un jugador a su equipo respecto al resultado del partido", ... "valorando el modo en cómo actúa alguien como equipo, no la actitud individual".
Ejemplo de Box-Score de la web acb.com. Recuperado de https://www.acb.com/partido/estadisticas/id/102997
- Eficiencia (EFF). En algunas competiciones, como la NBA, encontramos la métrica indirecta "indicador de eficiencia" (creada por Martin Manley) que permite, al igual que el indice de valoración, comparar rendimientos de los jugadores a partir de otras métricas directas, tales como puntos, rebotes totales, asistencias, balones robados, tapones a favor, balones perdidos y tiros intentados. En este caso se omiten otras métricas que si tienen en cuenta el índice de valoración, como las faltas recibidas o cometidas o los tapones en contra. Su formulación es la siguiente:
- Ratio de Eficiencia "Player Efficiency Rating" (PER). Otra alternativa es a los indicadores anteriores es la ratio de eficiencia del jugador desarrollado por John Hollinger. Dado la complejidad de este índice y las interpretaciones que se pueden realizar de el, éste será definido de forma independiente al Box-Score.
Ejemplo de Box-Score de la web nba.com. Recuperado de https://es.global.nba.com/boxscore/#!/0022100216
- Detalles
- Escrito por José Miguel Contreras
- Categoría: Glosario
La posesión, aunque la lógica incida en su simplicidad, es una de las métricas más importantes y su interpretación es fundamental, ya que, entre otros, permite interpretar otras métricas como el ritmo de juego (PACE), las eficiencias ofensiva y defensiva, etc., cuyos cálculos se basan en ésta.
¿Pero en realidad que es una posesión?
Se dice que un equipo tiene posesión cuando el balón cambia del equipo a éste, y ello va a ocurrir cada vez que un jugador del equipo contrario:
- Convierta un tiro de campo (de 2 o 3 puntos);
- Falle un tiro de campo y ese equipo no coja el rebote ofensivo;
- Pierda el balón (algunas fuentes agregan, para un cálculo de posesión más preciso, las "pérdidas de balón que se asignan a los equipos");
- Vaya a la línea de tiros libres para lanzar dos o tres tiros y anota el último tiro o lo falla, pero el equipo atacante no obtiene el rebote ofensivo del último tiro fallado.
Por tanto, una posesión comienza (Kubatko et al., 2007) cuando un equipo obtiene el control (o posesión) del balón y termina cuando ese equipo cede el control del balón. Los equipos pueden ceder la posesión del balón de varias formas, que incluyen (1) tiros de campo o tiros libres que hacen que el otro equipo saque la pelota fuera de límites del campo, (2) rebotes defensivos y (3) pérdidas de balón.
Hay que tener en cuenta que, según esta definición de posesión, un rebote ofensivo no inicia una nueva posesión; un rebote ofensivo inicia una nueva jugada.
¿Es una posesión lo mismo que una jugada?
Aunque lo parezca no son el mismo término. Se dice que empieza una nueva jugada cada vez que:
- Se ha producido un tiro de campo anotado o fallado;
- Se ha producido una pérdida de balón;
- Se ha producido una falta y se han de lanzar tiros libres o sacar de banda.
Por ejemplo, un equipo puede lanzar a canasta, fallar el tiro (finaliza la primera jugada), coger el revote ofensivo, lanzar de nuevo y fallar (finaliza la segunda jugada), coger el revote ofensivo, tirar y recibir una falta con la que ha de lanzar dos libres (finaliza la tercera jugada), anotando los dos (finaliza la posesión). Por tanto, solo se ha producido una posesión, pero se han desarrollado tres jugadas.
¿Cómo se calcula?
Existen dos formas de calcular (estimar) el número de posesiones (POS), una a la que llamaremos básica o tradicional y otra más específica.
Fórmula de posesión básica (eq. 1)
Donde:
TCIE = Tiros de Campo Intentados (Equipo)
PERE = Pérdidas (Equipo)
TLIE = Tiros Libres Intentados (Equipo)
ROE = Rebotes ofensivos (Equipo)
¿Qué son los valores 0,44 y 0,96?
Los multiplicadores 0,44 y 0,96 se utilizan para ponderar las posesiones en casos especiales que se pueden dar durante el partido (Kubatko et al., 2007):
- El ponderador 0,44 se usa dado que no todos los tiros libres acaban en posesión. Los tiros de faltas técnicas por ejemplo no lo hacen, mientras que puede haber más de dos tiros libres en una posesión. Un valor lógico sería tomar 0,5 ya que ponderaría los dos tiros libres tras una falta, pero como sabemos hay faltas de tiros de tres o dos más uno, situaciones que modificarían este valor. La investigación ha estimado que aproximadamente el 44% de todos los tiros libres acaban siendo posesiones.
- El ponderador de 0,96 tiene en cuenta situaciones del juego tales como que un jugador defensivo mande el balón fuera del campo en un rebote. En este caso continua la posesión sin que se sume un rebote ofensivo. O que el tiro se realice al final del cuarto y no se de la posibilidad de un rebote.
¿Se pueden estimar las posesiones de un equipo en función de los datos que aparecen en las estadísticas oficiales?
No es posible calcular al 100% las posesiones utilizando los datos de tablas estadísticas porque, entre otras razones, los tiros libres que finalizan la posesión no se identifican, algunos cuartos terminan sin rebotes ofensivos y no todos los rebotes se atribuyen a jugadores, por ejemplo, los tiros fallados que salen fuera del campo (a menudo tiros taponados), se registran como “rebote de equipo”.
Las posesiones se pueden "estimar" utilizando los datos de puntos de las estadísticas comúnmente disponibles. Una fórmula general para estimar las posesiones de un equipo es:
Donde:
TCIE = Tiros de Campo Intentados (Equipo)
TCCE = Tiros de Campo Convertidos (Equipo)
TLIE = Tiros Libres Intentados (Equipo)
TLCE = Tiros Libres Convertidos (Equipo)
ROE = Rebotes ofensivos (Equipo)
RDEO = Rebotes defensivos (Equipo Oponente)
PERE = Pérdidas (Equipo) 1
lamda = fracción de tiros libres que pone fin a las posesiones del total 2
alpha = valor entre (0,1)
1 incluye pérdidas de balón del equipo, como infracciones de 5 segundos o 24 segundos que no se atribuyen a ningún individuo. Estos se promedian alrededor de 0,666 por equipo y por partido.
2 Los tiros libres que ponen fin a las posesiones no incluyen los primeros tiros libres de dos, los primeros y segundos tiros libres de tres, o los tiros libres debidos a técnicas y faltas antideportivas. Además, los tiros libres después de los tiros de campo realizados no se cuentan, ya que el lanzamiento de campo realizado ya ha contado esa posesión. Se estima que el 43.8% de los tiros libres fueron tiros libres que terminaron con la posesión.
La ecuación anterior reconoce que cada pérdida de balón, canasta realizada o posesión efectuada tras un tiro libre constituye una posesión, es decir, tiene un valor de posesión de 1. Los intentos de tiros de campo fallados y los intentos de tiros libres fallados que finalizan la posesión comparten el valor de la posesión (1 punto) con los rebotes defensivos. Los intentos de tiros de campo fallados y los intentos de tiros libres fallados que finalizan la posesión obtienen una cuota alpha de ellos, mientras que el rebote defensivo obtiene una cuota 1 - alpha. Los rebotes ofensivos deshacen los intentos fallidos de tiros de campo y los tiros libres fallidos que terminan con la posesión, por lo que su valor de posesión es -alpha.
Nota: Si tomamos los valores de alpha = 1 y de lamda = 0,44 obtenemos la ecuación denomina “posesiones perdidas”, donde es importante señalar que implica que los rebotes defensivos no tienen valor de posesión. Otra formulación común, “posesiones ganadas”, asume que alpha = 0 e implica que los rebotes ofensivos, los intentos de tiros de campo fallados y los intentos de tiros libres fallados que terminan en posesión no tienen valor de posesión.
Otra fórmula "realmente simple" (para la NBA actual) es
Esta fórmula predice posesiones casi tan bien como más fórmulas complicadas.
¿Cómo medir las posesiones individuales?
De forma individual podemos medir las posesiones donde participa un jugador de ataque (no tiene sentido medir las defensivas). En este caso, podemos distinguir entre posesiones anotadas, que incluyen las que acaban en tiros anotados o asistidos, y no anotadas, tiros fallados o pérdidas.
Posesiones anotadas
Con
Posesiones no anotadas
Donde:
TCIJ = Tiros de Campo Intentados (Jugador)
TCCJ = Tiros de Campo Convertidos (Jugador)
TLIJ = Tiros Libres Intentados (Jugador)
TLCJ = Tiros Libres Convertidos (Jugador)
PERJ = Pérdidas (Jugador)
MINJ = Minutos (Jugador)
MINE = Minutos (Equipo)
ASE = Asistencias (Equipo)
Conclusiones
Las posesiones serán aproximadamente las mismas para dos equipos en un partido, por lo que éstas proporcionan una base útil para evaluar la eficiencia de equipos e individuos, aunque esta no sea una estadística registrada oficialmente en la mayoría de las ligas de baloncesto. Es por ello que, tanto equipos como jugadores van a intentar sumar más puntos por posesión que sus oponentes, ya que eso será un factor importante para alcanzar la victoria.
Nota: No se cuenta la posesión al final de un período cuando quedan menos o igual a cuatro segundos y no hay tiros de campo, tiros libres o pérdidas de balón.
Referencias
Kubatko, J., Oliver, D., Pelton, K., y Rosenbaum, D. T. (2007). A starting point for analyzing basketball statistics. Journal of quantitative analysis in sports, 3(3), 1-24.
Página 1 de 2